Задачи от Фибоначчи
Пизанский собирал эти задачи в разных странах. Большинство из них – арифметические и алгебраические примеры. Нужно повозиться с числами, извлекать корни, решать уравнения – и все в таком духе. Но есть и сюжетные и шуточные задачки с ситуациями из жизни – в них нужно выяснить стоимость или количество предметов, разделить имущество, следить за потомством и проводить финансовые расчеты между людьми (задачи коммерческой арифметики). Мы выбрали лишь некоторые из них.
Самая известная задача о кроликах
Задача о размножении кроликов, благодаря которой имя Леонардо Пизанского вошло в историю математики. В своем трактате по арифметике Liber abaci Фибоначчи впервые описывает эту задачу: «Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?»
Фибоначчи имел в виду взрослую пару кроликов, о чем говорит фраза «рождаются кролики со второго месяца». Если решать задачу для новорожденной пары, ответ будет другим.
Задача о семи старухах
Иллюстрация: www.paintingvalley.com
Эта задача известна во многих странах, самое раннее сведение о ней заметили в папирусе Ахмеса в Древнем Египте. Только у египетского писаря условия отличаются: «У семи лиц по семь кошек, каждая кошка съедает по семь мышей, каждая мышь съедает по семь колосьев ячменя, из каждого колоса может вырасти по семь мер зерна. Как велики числа этого ряда и как велика их сумма?»
В книге Пизанского упоминается и русский вариант этой задачи: «Шли семь старцев, у каждого старца по семь костылей, на каждом костыле по семь сучков, на каждом сучке по семь кошелей, в каждом кошеле по семь пирогов, в каждом пироге по семь воробьев. Сколько всего?»
Решение каждого варианта – это наглядный пример построения геометрической прогрессии и нахождения суммы первых n ее членов по известному первому члену и знаменателю.
Задачи о гирях
Найти пять гирь, с помощью которых можно взвесить любые грузы массой от 1 до 30 весовых единиц, но гири можно класть только на одну чашу весов. Решение строится в двоичной системе счисления.
Иллюстрация: www.vecteezy.com
Задача о птицах и монетах
30 птиц стоят 30 монет. Куропатки стоят по три монеты, голуби – по две, а пара воробьев – по монете. Сколько птиц каждого вида?
Эта задача может быть использована в другом варианте, но метод решения и ответ будут одинаковыми. Сплав из 30 весовых частей состоит из трех металлов: первый металл достоинством по три монеты на одну часть, второй металл по две монеты на одну часть, а у третьего металла каждые две части стоят по одной монете; стоимость всего сплава – 30 монет. Сколько частей каждого металла содержит сплав?
Иллюстрация: www.vecteezy.com
Задача о денариях
Если первый человек получит от второго семь денариев, то станет в пять раз богаче второго, а если второй человек получит от первого пять денариев, то станет в семь раз богаче первого. Сколько денег у каждого?
Римский денарий. www.oldbookillustrations.com
Задачи по теории чисел
а. Найти число, которое делится на 7 и дает в остатке единицу при делении на 2, 3, 4, 5 и 6.
б. Найти число, 19/20 которого равны квадрату самого числа.
Коротко
Полина Агеева
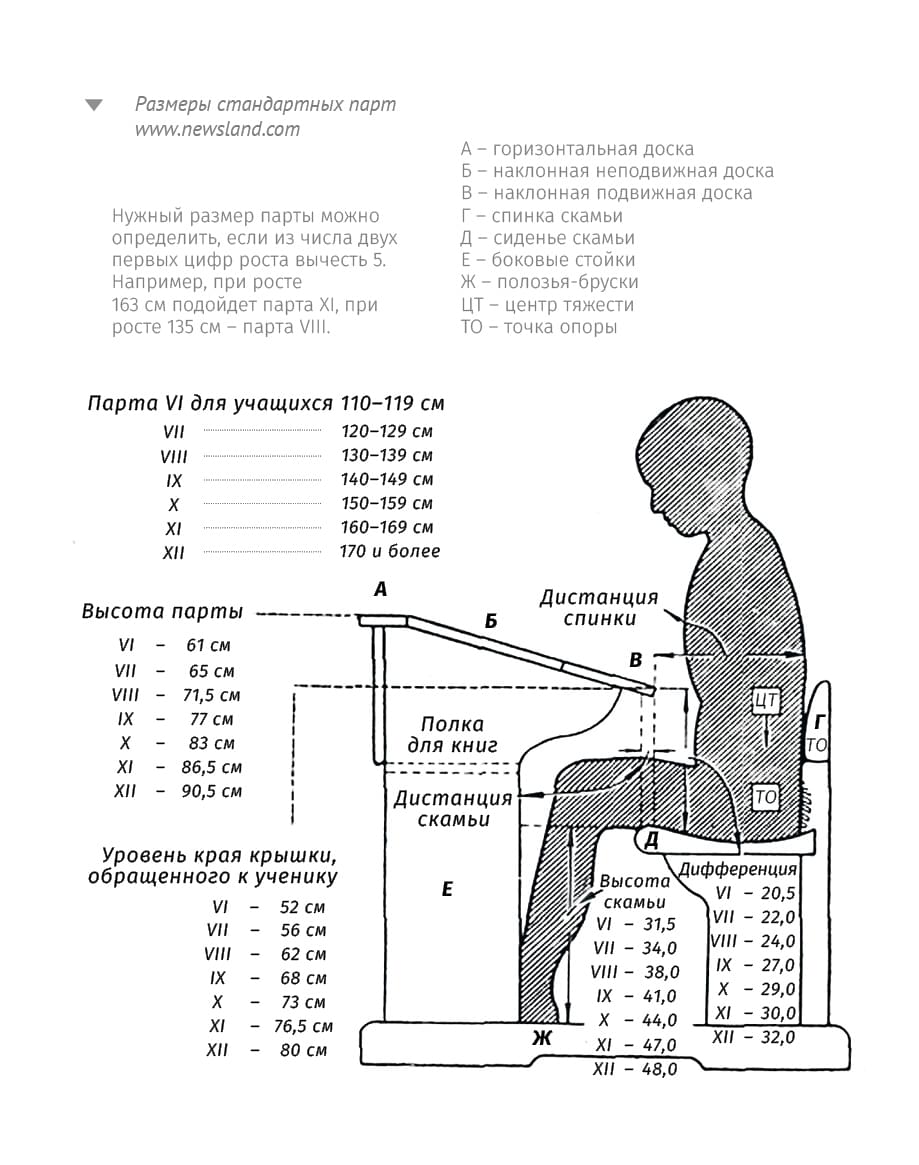Швейцарец Эрисман и новые парты для России
Игра в прятки с природой. Как сапиенсы придумали тёплую одежду
История Леонардо Фибоначчи. А был ли мальчик?
Числа Фибоначчи в искусстве
