Фракталы вокруг нас


Что такое фрактал
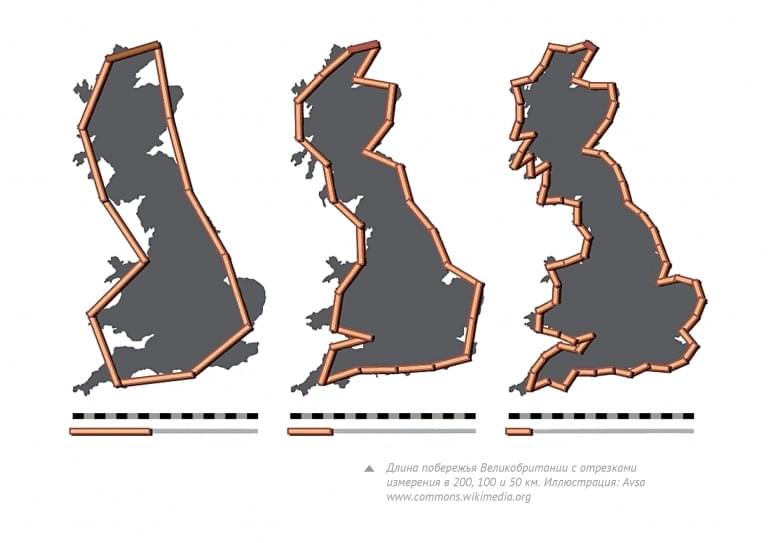
Предположим, что нам понадобилось измерить длину побережья какой-нибудь страны, например, Великобритании. Обычный метод – последовательно соединять две точки побережья линейкой на географическом атласе. Так же думал и английский ученый Льюис Фрай Ричардсон. Но, в отличие от других исследователей, он решил взять линейку покороче и измерить длину еще раз. И еще. И еще. И в каждом случае у него получалась разная длина! Казалось бы, здесь явно закралась ошибка. Однако, если мы внимательно посмотрим на изображение побережья Великобритании, то увидим, что Ричардсон был прав в своих подсчетах.
Длина измеряемой кривой зависит от масштаба измерений. И вот тут мы и подходим вплотную к понятию фрактала. Для обычной кривой при бесконечном уменьшении масштаба измерений ее длина станет постоянной. Например, для окружности таким образом можно получить формулу длины L = 2pR. Но длина побережья при постоянном уменьшении линейки будет неограниченно возрастать – это называется «парадоксом береговой линии», и именно с него началось научное изучение фракталов.
Если рассмотреть этот вопрос с физической точки зрения, то может показаться, что такое невозможно. Действительно, для реального, физического объекта мы не сможем бесконечно уменьшать масштаб измерений – рано или поздно мы дойдем до размеров атома. Однако из этого логичного рассуждения не следует невозможность существования фракталов – оно лишь показывает, что каждый объект обладает фрактальными свойствами лишь до определенного момента. И только математические объекты являются фракталами в полной мере и при любых измерениях. Из-за этой запутанности и сложности фракталов ученые обнаружили их как математический объект лишь во второй половине XX века. Хотя из примера с береговой линией очевидно, что они существовали и до этого, но только в 1975 году французский математик Бенуа Мандельброт написал книгу о фракталах и фактически основал теорию фракталов в недавно возникшей области науки – теории хаоса.
Однако еще до выхода книги, в 1967 году в журнале Science была опубликована его статья «How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension» о парадоксе береговой линии. В статье ни разу не встречается слово «фрактал», хотя именно она считается стартовой точкой для фрактальной геометрии. Мандельброт решает этот парадокс удивительным образом – он заявляет, что нельзя говорить о таком понятии, как «длина береговой линии», в привычном нам понимании. Чтобы доказать свое утверждение, он вводит ключевое для теории фракталов понятие фрактальной размерности. Самое странное в ней то, что она не является целой!
В математике размерностью обычно называют топологическую размерность, которая просто-напросто соответствует количеству измерений предмета. Так, куб имеет три измерения – длину, ширину и высоту, следовательно, его размерность равна трем. А линия на бумаге имеет только длину, и ее размерность равна единице. Поэтому на первый взгляд кажется невозможным представить предмет с нецелой размерностью. Какой объект может иметь размерность 1,26? А ведь его описали еще в 1904 году и более полувека попросту не обращали на него внимания, считая забавной игрушкой. Это снежинка Коха, представляющая собой замкнутую кривую с простейшим алгоритмом построения, из которого ясно, что ее длина в привычном нам понимании бесконечна. Математики ввели для такой нецелой размерности отдельный термин – размерность Хаусдорфа-Безиковича.
Также можно заметить схожесть этой снежинки с изрезанной береговой линией – каждый ее фрагмент в крупном масштабе подобен ее же более мелкому фрагменту. Это свойство называется самоподобием – оно ключевое для всех фракталов. Из аналогии с береговой линией мы можем получить интуитивное понимание нецелой размерности – ее можно описать как «степень изрезанности кривой».
 Губка Менгера. Иллюстрация: Niabot, www.de.wikipedia.org
Губка Менгера. Иллюстрация: Niabot, www.de.wikipedia.org
Из-за неоднозначного понимания фракталов существует целое множество их определений. Наиболее общее, предложенное Мандельбротом, гласит, что фракталом называют структуру, состоящую из частей, которые в каком-то смысле подобны целому. При этом фрактал не обязательно должен быть кривой, как в предыдущих примерах, – это может быть как плоская, так и объемная фигура. Например, фракталами являются ковер Серпинского или губка Менгера.
Развитие теории фракталов тесно связано с ее основателем, Бенуа Мандельбротом – в одиночку он долгое время отстаивал и доказывал свою идею всему научному сообществу. Поэтому история открытия фракталов – в значительной степени биография Бенуа Мандельброта, хотя частные случаи фракталов (множества Жюлиа, снежинка Коха и функция Вейерштрасса) были известны и раньше. Но только Мандельброт увидел что-то общее в этих примерах и дал им описание.
 Бенуа Мандельброт. Фото: Yale University, www.spektrum.de
Бенуа Мандельброт. Фото: Yale University, www.spektrum.de  Множество Жюлиа, www.eldar.mathstat.uoguelph.ca
Множество Жюлиа, www.eldar.mathstat.uoguelph.caВ последующие годы Мандельброт вихрем проносился по разным областям науки, от физики до биологии, в каждой из них находя подтверждение своим теориям. В то же время научным сообществом его исследования воспринимались как нечто недостойное внимания. Отчасти это происходило из-за недостаточной на тот момент формальности теории, отчасти – из-за ее разрозненности. Большинство ученых просто не понимали, как и для чего можно применять эту теорию. Однако это не помешало ее дальнейшему развитию.
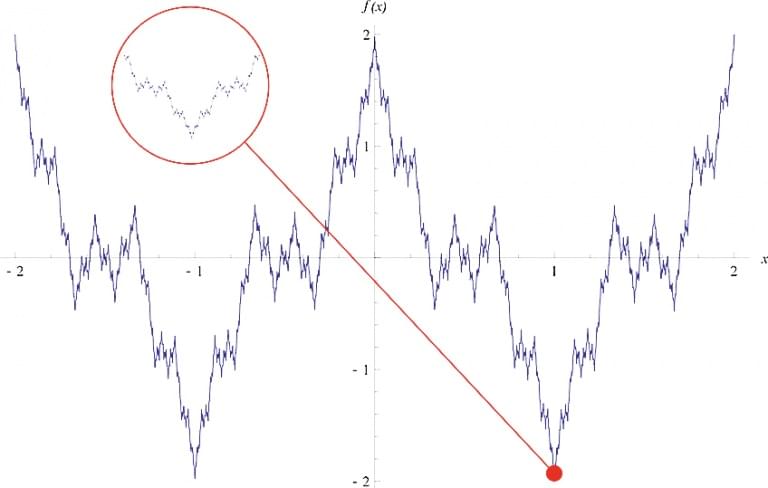 Функция Вейерштрасса. Иллюстрация: Eeyore22, www.ru.wikipedia.org
Функция Вейерштрасса. Иллюстрация: Eeyore22, www.ru.wikipedia.org Фракталы вокруг нас
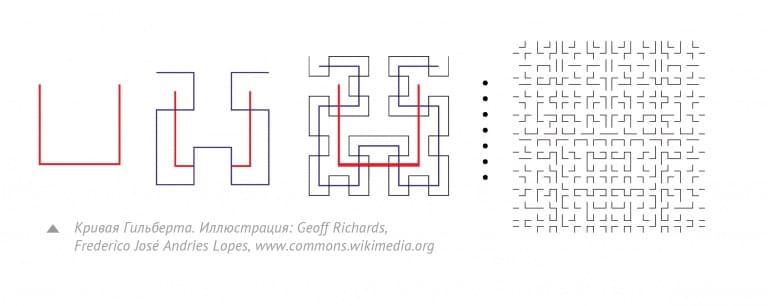
За время, прошедшее с выхода первых работ Мандельброта, фракталы получили множество применений. Сама же теория проделала долгий путь от рисования занимательных и необычных фигур и поиска их аналогов в реальном мире до практического использования при решении серьезных научных задач.Например, одно из свойств фракталов основано на их способности иметь дробную размерность. Рассмотрим в качестве примера необычную кривую Гильберта с размерностью, очень близкой к 2, и нарисуем ее на плоскости. Она будет настолько извилистой, что полностью займет всю предоставленную ей плоскость, при этом оставаясь кривой с бесконечной длиной. Аналогично можно представить объемную структуру с небольшим объемом и бесконечной площадью – это человеческие легкие. Способность поглощать кислород напрямую зависит от площади дыхательной поверхности легких, но при этом они должны занимать относительно небольшой объем. Именно поэтому небольшие человеческие легкие имеют дыхательную поверхность большую, чем стандартный теннисный корт.
Теорию фракталов используют в материаловедении. Шероховатости и неровности, остающиеся на поверхности любого металла после его полировки или изготовления, имеют фрактальную природу. И более того, по ним можно предсказать прочностные характеристики металла – существует прямая зависимость между фрактальной размерностью и энергией, необходимой для разрушения металла. Аналогичные результаты были в исследованиях полимеров. Оказалось, что полимерные цепочки образуют сложные и запутанные структуры, которые определяют ключевые показатели полимеров. И эти запутанные цепочки – тоже фракталы!
Отдельное развитие получили алгоритмы для генерации фракталов. Часть из них придумали еще в XIX веке, другие появились, когда возникла теория фракталов. Вместе они стали основой раздела в искусстве, посвященного фрактальным узорам. Вскоре выяснилось, что можно генерировать компьютерную графику при помощи фракталов. Особенно актуально это оказалось для биологических структур: деревьев и растений. У капусты Романеско, например, невооруженным глазом видна фрактальная структура.
 Капуста романеско, www.fr.freepik.com
Капуста романеско, www.fr.freepik.com У применения фракталов есть и весьма неоднозначные истории. В начале 90-х годов появились алгоритмы фрактального сжатия изображений, обещавшие огромную степень сжатия, но требующие большого количества времени. Такие алгоритмы ищут на картинке самоподобные участки, кодируют их специальным образом и значительно уменьшают размер изображения. К сожалению, их развитие замедлилось в самом начале из-за того, что несколько основных и перспективных алгоритмов были запатентованы группой открывших их ученых. Патенты описывали метод сжатия достаточно общими чертами, и многие новые алгоритмы попадали под их ограничения. В 2012 году срок действия части патентов закончился, и фрактальное сжатие изображений продолжает развиваться вновь после долгого перерыва.
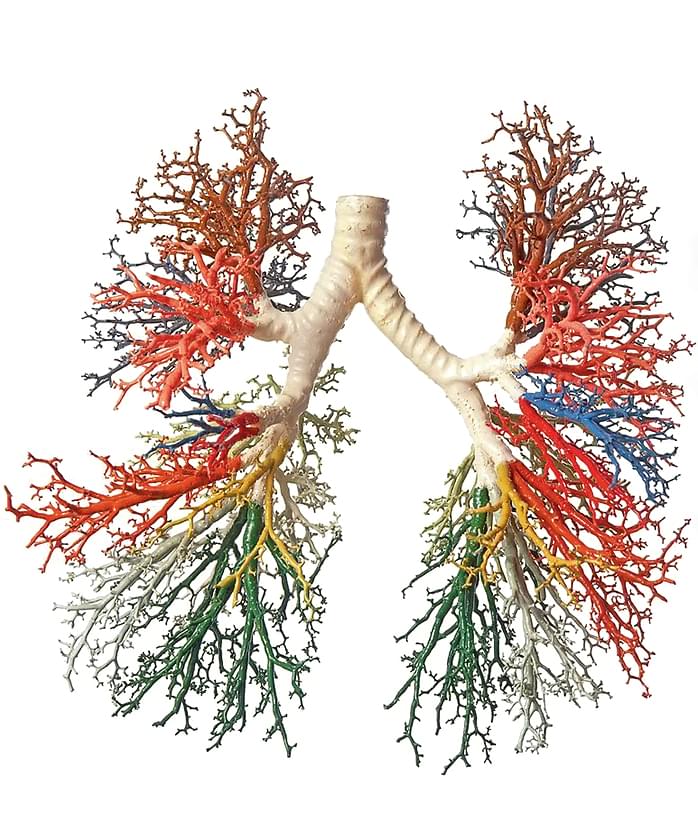 «Дерево» бронхов. Фото: Dorling Kindersley/uig, www.fineartamerica.com
«Дерево» бронхов. Фото: Dorling Kindersley/uig, www.fineartamerica.comА исследования цен на хлопок, с которых начинал Мандельброт, переросли в отдельное направление в экономике – фрактальный анализ рынка. С его помощью экономисты предсказывают цены на бирже и строят финансовые модели. Сам же Мандельброт после выхода его книг про фракталы наконец получил заслуженное признание в академической среде. Однако он так и не остановился ни на математике, ни на физике, ни на какой-либо еще области науки, продолжая переходить от одной задачи к другой.
Теория фракталов – это не только про необычные изображения, но и про борьбу и упорство одного ученого, который смог собрать воедино разрозненные знания из разных областей науки, увидеть в них что-то общее и создать принципиально новую науку. И все это несмотря на скептическое отношение большинства коллег, долгое время не хотевших принимать фракталы.
Автор: Глеб Кузьмин
Наука
Глеб Кузьмин




 Сыны скво: как жили индейцы
Сыны скво: как жили индейцы Надменные потомки: как изменится человек к концу XXI века
Надменные потомки: как изменится человек к концу XXI века Числа Фибоначчи: что, как и почему
Числа Фибоначчи: что, как и почему









