Булочка с изюмом: теория хаоса в быту


Иллюстрация: Erika Iris www.flickr.com
В термодинамике существует такой парадокс: если взять сосуд с газом, отделенным перегородкой от другой части сосуда с вакуумом, а потом перегородку убрать, то однажды все частицы газа снова окажутся в той же области, где были в начале. Это утверждение кажется практически невозможным, ведь в нем даже ничего не говорится про объем сосуда. А если в этом газе миллиарды частиц? Парадокс в том, что в нем ничего не говорится о времени. Да, газ действительно вернется в начальную половину сосуда, но это может произойти и через десять, и через сто лет, а более точные оценки времени, в зависимости от размера сосуда, могут даже превышать возраст Вселенной.
Этот парадокс – прямое следствие теоремы о возвращении математика и физика Анри Пуанкаре. В упрощенной формулировке эта теорема говорит о том, что любая система вернется в окрестность своего начального состояния. Теорема о возвращении – один из первых ростков теории хаоса. Теория хаоса мультидисциплинарна. Ее можно представить как дерево с множеством корней, и все они – области знания, из которых зародилась новая наука.
Анри Пуанкаре
Эффект бабочки и детерминизм Лапласа
Следующим значимым шагом в становлении теории хаоса (после теоремы о возвращении) были исследования Лоренца, в результате которых он открыл широко известный «эффект бабочки». В середине XX века Эдвард Лоренц занимался метеорологией и пытался составить модель земной атмосферы. В то время физики считали метеорологию прикладной и бесперспективной наукой: делать прогнозы по таблицам на несколько дней можно было научить кого угодно. Но Лоренцу просто нравилось составлять различные модели, да и появившиеся компьютеры, которые также никто не принимал всерьез, значительно в этом помогали. Именно Лоренц в конце концов поставил точку в теории детерминизма. Но как философская теория детерминизма связана с наукой? Чтобы в этом разобраться, перенесемся на несколько веков назад.
Лаплас
Во времена Лапласа значительная часть ученых придерживалась принципов абсолютного детерминизма – это согласовывалось с имеющимися знаниями о мире и обещало в обозримом будущем объяснить все физические законы. Отчасти успех детерминизма был продиктован огромными успехами ньютоновской механики, позволившей за одно столетие совершить огромный скачок в науке. Основным принципом ньютоновской механики являлось описание всех физических процессов набором дифференциальных уравнений. То есть, зная набор уравнений и некие дополнительные данные, называемые начальными условиями, можно было предсказать параметры системы в любой другой момент времени. Именно по этим принципам и сейчас рассчитываются орбиты планет, спутников и космических аппаратов. Лаплас возвел принципы ньютоновской механики в абсолют: он предположил существование демонов Лапласа. Суть такого демона в простом утверждении: зная начальные условия для всех частиц во Вселенной, он может предсказать параметры этих частиц в любой следующий промежуток времени. Очевидно, что если такой демон существует, то из этого напрямую следует предопределенность любого действия во Вселенной.
В начале XX века теорию детерминизма пошатнуло появление квантовой механики, в особенности открытие принципа неопределенности Гейзенберга – он говорит о том, что невозможно одновременно точно измерить координату и импульс частицы. Но окончательно добил теорию детерминизма именно «эффект бабочки» Лоренца. Когда в 60-х годах он составлял модели для предсказания погоды, все расчеты показывали, что модель действительно хорошо описывает реальные явления в атмосфере, но при этом через некоторое время симуляция начинала все сильнее отличаться от реальности. Однажды Лоренц округлил последний знак одного из начальных условий уравнений и через несколько часов увидел другую картину атмосферы, которая абсолютно не совпадала с реальностью, – малейшая ошибка в начальных условиях привела к совсем другому решению уравнений и к совершенно другому развитию событий. Именно этот эффект в дальнейшем и назовут «эффектом бабочки» – взмах крыльев бабочки в одном конце земного шара может привести к образованию урагана в другом.
Когда Лоренц понял, чем вызвано странное развитие его модели, он сразу догадался, почему его модель в итоге всегда расходилась с реальной атмосферой. Дело в том, что в компьютере было ограничение на размер знаков числа после запятой, – а начальные условия для уравнений нужно было определять с гораздо большей точностью, чем позволял компьютер. Кажется, что это условие можно обойти на современных компьютерах, но здесь вновь появляется принцип неопределенности Гейзенберга: даже если программе можно будет задать параметры с нужной точностью, мы не сможем измерить их с требуемой правильностью. На практике же из-за «эффекта бабочки» невозможен долгосрочный прогноз погоды.
Предсказание будущего и аттракторы
Среди остальных областей науки теория хаоса отличается удивительно красивыми и наглядными результатами – это геометрические фракталы, аттракторы или турбулентность. Аттракторы заслуживают отдельного внимания. Сам по себе аттрактор с физической точки зрения – это всего лишь схема динамики некой системы в интересующих нас координатах. Например, простейший аттрактор может показывать изменение скорости и координаты тела. А в более общем случае может описывать любые параметры – от силы тока в цепи до количества волков в стае. Рецепт построения аттрактора тоже достаточно прост. Нужно взять систему дифференциальных уравнений, описывающих изменение системы во времени, получить решение этой системы и построить график, причем переменная времени из этого решения исключается.
С теорией хаоса наиболее тесно связаны странные аттракторы – аттракторы с фрактальной структурой, описывающие системы с хаотическим поведением. Один из самых известных странных аттракторов открыл тот же Эдвард Лоренц. Интересная особенность аттрактора Лоренца в том, что он охватывает целый ряд физических явлений. Например, с его помощью можно описать конвекцию (перемешивание) воды в плоском слое и работу простейшего лазера.
Пожалуй, самые неожиданные области применения теории хаоса – экология и биология. При помощи методов, используемых при построении аттракторов, ученые смогли визуализировать аттрактор для модели эпидемии кори.
Здесь может возникнуть вопрос – а зачем вообще это нужно? Как было сказано, аттрактор показывает динамику развития системы. Значит, если у нас есть модель системы или ее аттрактор, то мы можем найти на аттракторе наиболее подходящую текущему состоянию точку. И, зная ее, можем определить следующую точку, то есть следующее состояние системы. Говоря более простым языком, мы фактически получаем предсказание будущего!
Конечно, зачастую это предсказание не совсем точное, но даже это уже большой успех. И вполне очевидно, что такие предсказания нужны во всех областях науки. Например, один из ученых, разработавших метод предсказания популяции планктона, – Джордж Сугихара на некоторое время занялся исследованиями в финансовой области, и теперь его разработки применяются в автоматизированной торговле акциями.
Теория хаоса и радиофизика
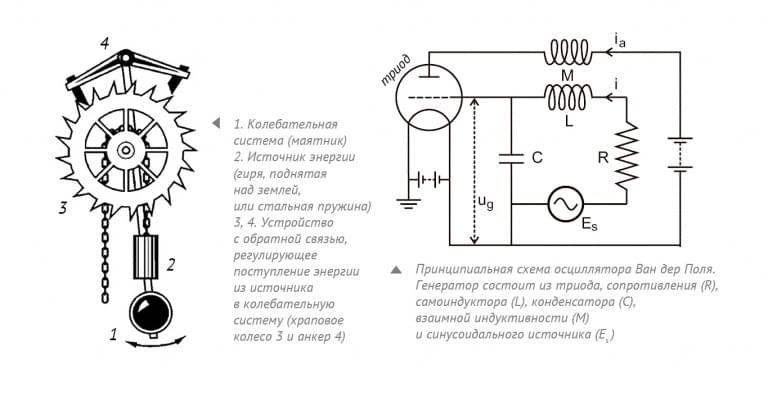
Не только математика и биология привели к образованию теории хаоса – множество задач пришло в эту науку и из различных областей физики, от гидродинамики до радиофизики. В 1927 году голландский физик Балтазар ван дер Пол начал исследовать осциллятор (генератор), позже названный его именем, – пример нелинейной системы с автоколебаниями. Автоколебания – это вид колебаний с трением, в котором колебания поддерживаются за счет постоянного подвода энергии. Простейший пример таких колебаний – маятник на часах: колебания в нем должны остановиться за счет действия силы тяжести, но маятник продолжает движение за счет подвода энергии (например, за счет постепенного опускания гири). Нелинейность в генераторе Ван дер Поля возникает из-за того, что затухание колебаний в нем происходит не линейно, а с коэффициентом, в котором есть переменная уравнения.
При исследовании генератора Балтазар ван дер Пол обнаружил, что при периодическом внешнем воздействии наблюдаются области частот с шумами, находящиеся рядом с собственными частотами, что является проявлением хаоса! Также при работе осциллятора возникают предельные циклы – стационарное состояние системы.
Тогда же, в конце 20-х годов, советский физик Александр Андронов установил, что вообще все периодические автоколебания в математическом смысле являются предельными циклами. Благодаря этим открытиям возникла нелинейная теория колебаний – наука, исследующая «сложные» колебания и значительно пересекающаяся с теорией хаоса. И, как во многих других примерах, исследования Ван дер Поля пригодились не только в физике, но и перетекли в биологию – на основе полученных им уравнений создана одна из моделей нейрона (модель ФитцХью–Нагумо).
 Фазовый портрет осциллятора Ван дер Поля. Красная линия – предельный цикл
Фазовый портрет осциллятора Ван дер Поля. Красная линия – предельный цикл
Практическое применение теории хаоса
Все эти дисциплины: математика, гидродинамика, радиофизика, биология и многие другие – привели к образованию теории хаоса как отдельной науки. И сейчас она находит все больше применений в различных задачах, порой очень необычных. Например, на основе теории хаоса строится клиодинамика – междисциплинарная наука, которая занимается математическим моделированием исторических процессов. Основная цель этой науки – понять процессы развития человечества: возвышение и падение цивилизаций и государств, динамику населения и распространение религий. Например, один из основателей клиодинамики, Петр Турчин, составил модель, определяющую промежуток времени между двумя последующими кризисами в государстве. В теории такие модели могут предсказать дальнейшее развитие истории! И хотя сейчас перспективы клиодинамики с точки зрения многих ученых весьма сомнительны, кто знает, во что в дальнейшем может перерасти эта наука? Может, в ближайшем будущем мы сможем предсказывать развитие всего человечества на годы или даже на века вперед, как это было у Азимова в «Основании».
В качестве другого примера можно привести моделирование лесных пожаров. Один из подходов к этой задаче состоит в создании клеточной модели леса, где каждому дереву соответствует отдельная клетка, а вероятность пожара зависит от наличия рядом горящих деревьев и некоторых дополнительных факторов – это можно представить как некий морской бой, в котором при попадании могут загораться стоящие рядом корабли.
Теория хаоса стала большой междисциплинарной наукой. Более того, именно в теории хаоса ученые впервые перешли к рассмотрению сложных систем, а не их простейших составляющих, чем зачастую ограничивались раньше. Главным же стимулом для развития этой науки стало появление очень похожих задач в абсолютно разных областях. А фактором, обусловившим развитие теории хаоса, стало широкое распространение компьютеров – без них большая часть расчетов была бы невозможна.
Но, пожалуй, самое важное следствие теории хаоса – расширение междисциплинарных исследований. Много проблем в биологии и экологии было решено с помощью новых математических моделей, и наоборот – некоторые математические модели (например, нейронные сети) были вдохновлены биологическими объектами. И теперь в мире все больше ученых занимаются не математикой или физикой, а чем-то средним между многими областями наук. И зачастую такой подход помогает решить задачи, долгое время считавшиеся сложными, а то и нерешаемыми.
Наука
Глеб Кузьмин









 Homo бушменос
Homo бушменос Синтезируя жизнь
Синтезируя жизнь Числа Фибоначчи: что, как и почему
Числа Фибоначчи: что, как и почему Наука без правил: квантовая физика
Наука без правил: квантовая физика








