Числа Фибоначчи: что, как и почему

Иллюстрация: www.pinterest.cl/northcoteart

Отец Фибоначчи желал, чтобы его сын, как и он сам, стал торговцем. Но, к счастью для науки, Леонардо пошел другим путем. Сейчас мы знаем Фибоначчи в первую очередь по последовательности чисел, опубликованной им в его первом трактате Liber аbaci. Но в нем есть кое-что гораздо более значимое для современной западной науки – в этой книге Фибоначчи один из первых описал использование системы счисления с индийскими цифрами. Значимость последующего перехода к индийской позиционной системе сложно переоценить – большая часть современных открытий базируется на математических расчетах, многие из которых весьма затруднительны в римской системе счисления. В качестве примера можно рассмотреть простейшие арифметические действия – умножение и деление. В привычной нам системе счисления все просто – нужно всего лишь вспомнить таблицу умножения и переносить числа из одного разряда в другой. Но в случае с римской системой такой фокус уже не сработает – если с умножением еще как-то можно справиться, то представить себе деление числа DCXXXVI на число LIII уже гораздо сложнее. Другой пример – это вся современная вычислительная техника, использующая в основном двоичную позиционную систему счисления.

Поскольку деление было очень сложным действием в римской системе счисления, для этого использовали специальный инструмент – абак 

Однако вернемся к числам Фибоначчи. Несмотря на решение стать ученым, Леонардо так и не забыл того, что изначально должен был стать торговцем. Может быть, поэтому юный математик включил в свой трактат множество практических примеров, особенно полезных именно для купцов и продавцов. В частности, Фибоначчи неоднократно демонстрировал, как использование индийской системы счисления и дробей позволяет упростить и ускорить частую задачу для торговцев того времени – перевод всевозможных единиц измерения в привычные купцам единицы и валюты. С другой стороны, Леонардо Пизанский уделил значительную часть своей книги и более отвлеченным задачам – именно так и была выявлена последовательность чисел Фибоначчи.

Одна из задач, поставленных математиком, звучала так: если любая пара кроликов производит новую пару каждый месяц, начиная со второго месяца существования, то сколько пар кроликов мы получим через год? При этом считается, что в начале у нас есть одна такая пара кроликов, и животные не умирают. Рассмотрим для примера первые несколько месяцев развития популяции таких кроликов.

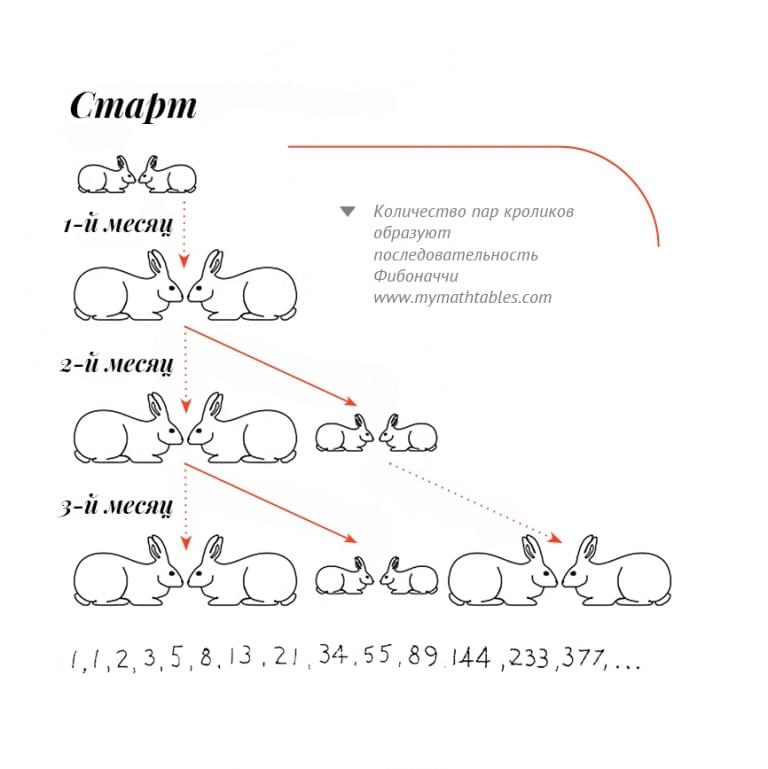
Итак, мы начинаем с одной пары кроликов. В конце первого месяца у нас все еще одна пара. В конце второго месяца у нас есть стартовая пара кроликов и еще одна пара, родившаяся у них. К концу третьего месяца изначальная пара кроликов производит еще одну пару – в итоге мы имеем уже три пары кроликов. На этом шаге мы можем получить формулу для количества пар кроликов к концу следующего месяца – оно будет равно количеству пар в конце текущего месяца плюс их количество в конце предыдущего месяца. Зная эту формулу, мы легко можем вычислить количество пар кроликов к концу каждого месяца и получить последовательность Фибоначчи, как это сделал в свое время Леонард Пизанский. Вот искомая последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … Однако легко заметить, что данный пример имеет мало общего с реальностью – как минимум кролики все-таки не бессмертны. Но есть и другие, гораздо более реалистичные случаи применения последовательности Фибоначчи в природе: родословная пчел, раковины моллюсков, соцветия растений, ДНК человека.

Главное, что нужно уяснить из задачи о кроликах: числа Фибоначчи – это числовая последовательность, в которой каждое новое число равняется сумме двух предыдущих. А как она применяется на практике?

Числа Фибоначчи и золотое сечение

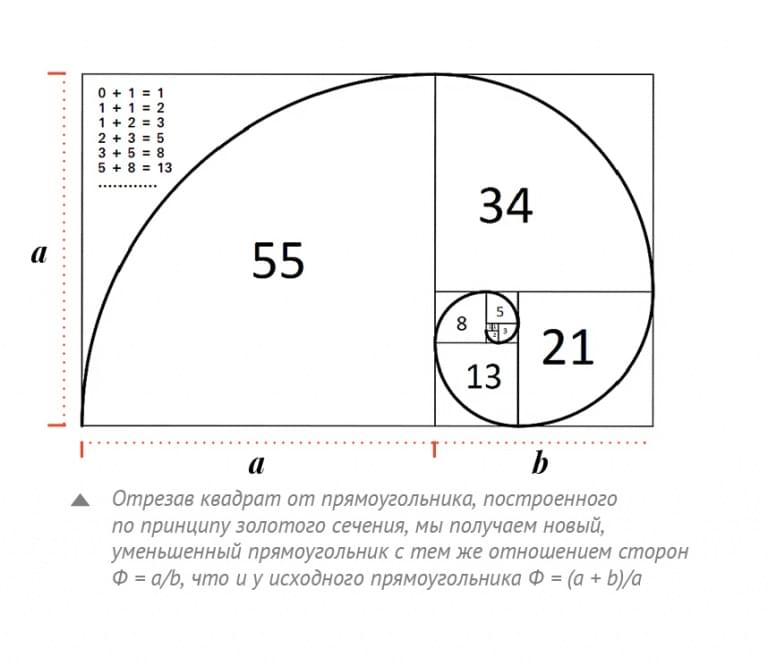
В математике на основе последовательности Фибоначчи можно построить набор квадратов со сторонами, равными элементам этой последовательности. Добавляя каждый квадрат из этого набора к сторонам двух предыдущих квадратов, мы всегда будем получать прямоугольник, стороны которого равны двум последующим числам Фибоначчи. И, наконец, если мы решим вписать в каждый из этих квадратов по четверти окружности, то мы получим аппроксимацию широко известной золотой спирали, используемой в архитектуре. На первый взгляд это описание может показаться сложным, но если взглянуть на рисунок, все сразу встает на свои места.

В этом примере наиболее ясно видна связь последовательности Фибоначчи и золотого сечения, которое используется для построения золотой спирали. Но существует и еще более явная взаимосвязь между числами Фибоначчи и золотым сечением – последнее можно напрямую получить из соотношения двух чисел Фибоначчи! Как известно, золотое сечение – это иррациональное число (то есть его нельзя выразить рациональными дробями – говоря более простым языком, это число с бесконечным числом знаков после запятой), приблизительно равное 1,618. А теперь попробуем делить каждое следующее число Фибоначчи на предыдущее, начиная с единицы: 1/1 = 1; 2/1 = 2; 3/2 = 1,5; 5/3 ≈ 1,666; 8/5 = 1,6; 13/8 = 1,625. Продолжая такие вычисления, мы будем все ближе и ближе приближаться к реальному значению золотого сечения!

Последовательности на базе чисел Фибоначчи

За века изучения чисел Фибоначчи ученые придумали множество вариаций классической последовательности. Например, зная формулу для чисел Фибоначчи, можно посчитать числа, которые должны предшествовать единице, тогда мы получим последовательность Фибоначчи с отрицательными членами:

…, –8, 5, –3, 2, –1, 1, 0, 1, 1, 2, 3, 5, …

Другой способ модифицировать последовательность Фибоначчи – складывать для получения следующего члена не два предыдущих, а три, четыре или еще больше элементов. В случае трех членов последовательность будет называться числами трибоначчи и иметь следующий вид:

0, 0, 1, 1, 2, 4, 7, 13, 24, 44, …

В итоге многовековых исследований числа Фибоначчи и полученные из них последовательности стали одними из самых изученных в теории чисел. Неудивительно, что помимо вышеприведенных примеров существует огромное количество практических применений чисел Фибоначчи.

«Случайные» числа Фибоначчи

Один из самых необычных примеров использования чисел Фибоначчи в современной математике и информатике – генерация псевдослучайных чисел. Для исследователей во всех областях наук последнее время очень важным является вопрос о случайных числах. Но что же такое случайное число?

Не вдаваясь в сложные математические выкладки, можно понять это на простом примере. Предположим, вам надо сделать выбор между двумя блюдами – например, гречкой и макаронами. При этом каких-либо явных предпочтений у вас нет. Очевидное решение – бросить монетку и решить, что будет соответствовать орлу, а что – решке. Если же вы скажете, что орел – это единица, а решка – ноль, то при помощи подбрасывания монетки сможете получить некое число. Именно число, поставленное в соответствие некому исходу события, и будет являться случайным числом, или, если говорить более научно, случайной величиной. Другой пример получения случайной величины – это бросание кости, у которой каждый результат соответствует числу от 1 до 6.

На первый взгляд действительно кажется, что для получения случайного числа достаточно всего лишь бросить монетку или игральную кость N число раз. До изобретения компьютеров люди зачастую обходились именно таким методом. Но с появлением первых вычислительных машин и усложнением научных задач ученым во всех областях науки требовались все большие и большие количества случайных чисел. Наиболее важны эти числа оказались для специалистов в области численного моделирования и оптимизации – именно для их экспериментов в первую очередь требовались огромные массивы случайных чисел. Косвенным примером важности и необходимости этих чисел служит очень популярная в XX веке книга A Million Random Digits with 100,000 Normal Deviates американского аналитического центра RAND, которая издавалась на протяжении полувека. Ее основным содержанием был миллион случайных чисел, записанных по 2500 чисел на страницу.

Игра в кости во время древнеримского праздника Сатурналии. Римская фреска в Помпеях